The significant figures calculator solves expressions with sig figs and changes any number into a new number with the required number of sig figs (try 3.14 / 7.58 – 3.15). Which rules apply to significant figures? This page will go over those ideas in detail as well as show you how to use a sig fig calculator.
How to utilize this calculator for major figures?
Allow us to assist you in making the most use of this calculator:
Put a number or phrase in here
The findings, including the number in decimal notation and the number of significant figures in the number (or expression), will be promptly summarized by the significant figures calculator. Enter the required significant figures in the round to sig fig field to reduce this number to a different amount of significant figures. The number is immediately rounded to the designated significant figures in the findings.
You can choose a different rounding method if you’d like, although half up is the default. Click on the Advanced mode to accomplish this. This will create a new field called “rounding mode,” with a variety of possibilities. Think about the number 24.0725, for instance. The significant figures calculator indicates that a number has six significant numbers when we enter 24.0725. It also displays the scientific notation (2.40725 × 101), the E-notation (2.40725e+1), and the decimal notation. Assume that for this number, we only want three significant figures. The decimal notation 24.1 appears in the results area as soon as we enter 3 in the round to sig-fig box.
What numbers are noteworthy?
All figures that contribute to the overall meaning of the number are considered significant. To avoid repeating insignificant quantities, numbers are frequently rounded. When rounding, one has to be careful not to lose accuracy. Simplifying numbers is frequently the main objective of rounding them. Use the rounding calculator to help solve these kinds of issues. Math Playground will help you to resolve the issues.
Which rules apply to significant figures?
Apply the subsequent guidelines to ascertain which numbers are important and which are not:
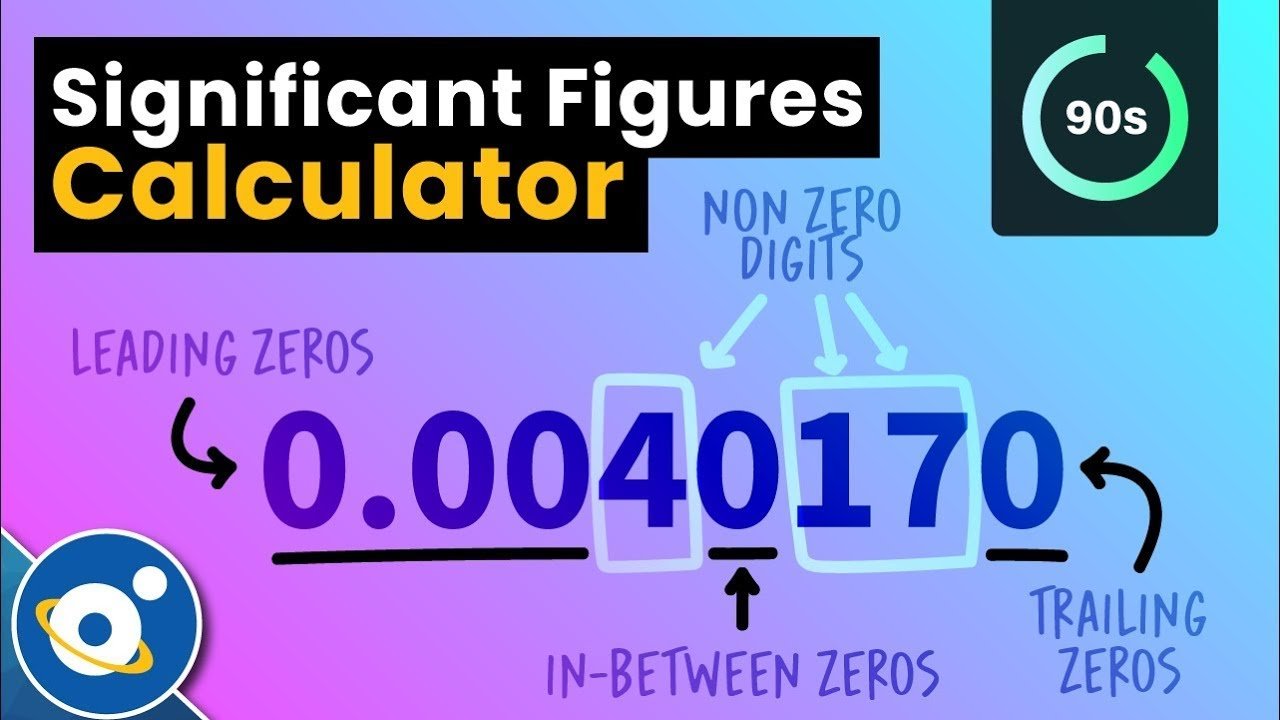
- A decimal value less than one does not have a significant zero to the left of it.
- There is no significance to any trailing zeros that are placeholders.
- There are important zeros in between non-zero values.
Every non-zero number has meaning.
A number is rounded if it has more digits than the intended number of significant digits. For instance, 432,500 equals 433,000 to three significant digits when rounding to the nearest half (regular).
Non-significant zeros at the end of numbers are left in place since eliminating them would change the number’s value. We are unable to eliminate the 000 in 433,000 from the example above without first converting the value to scientific notation.
Additional illustrations of the sig fig calculator’s application
Our significant figures calculator has two modes of operation: it may round a number to the number of significant figures you want or conduct mathematical operations on several integers (e.g., 4.18 / 2.33).
We can compute sig figs manually or with the help of the significant figures counter by following the above-mentioned guidelines. Assume that we require two significant figures and that the number is 0.004562. As placeholders, the trailing zeros are not counted. We next round 4562 to two digits, which gives us 0.0046.
We’ll now look at an example that doesn’t involve a decimal. Assume that 3,453,528 to 4 significant digits are what we seek. We get 3,454,000 by simply rounding the whole amount to the closest thousand.
What happens if a figure has scientific notation?
The same guidelines apply in these situations. Use E notation to input scientific notation into the sig fig calculator. This involves substituting × 10 with a capital or lowercase letter “e.” For instance, 5.033E23, often known as 5.033e23, is equal to 5.033 x 10²³. The E notation representation for a very small number, such as 6.674 x 10⁻¹¹, is 6.674E-11 (or 6.674e-11). The scientific notation calculator contains additional information about this convention.
When estimating, one should round to the nearest integer and limit the number of significant digits to the log base 10 of the sample size. For instance, if the sample size is 150, we use two significant numbers because the log of 150 is roughly 2.18.
Conclusion
The number in the operation with the least precision should be the only decimal place in the result for addition and subtraction operations. For instance, the value with the fewest decimal places (1) is 128.1 when the operation 128.1 + 1.72 + 0.457 is carried out. Because of this, the outcome also needs to be expressed to one decimal place: 128.̉1 + 1.7̲2 + 0.45̲7 = 130.̉277 = 130.̉3. The final significant number is highlighted to show its place.